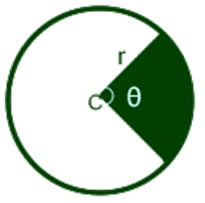
Medindo a área do arco de um círculo
A área total de um círculo é proporcional ao tamanho do raio e pode ser calculada pela expressão π * r², na qual π equivale a 3,14 e r é a medida do raio do círculo. O círculo pode ser dividido em infinitas partes, as quais recebem o nome de arcos (partes de um círculo). Os arcos de uma região circular são determinados de acordo com a medida do ângulo central, e é com base nessa informação que calcularemos a área de um segmento circular.
Uma volta completa no círculo corresponde a 360º, valor que podemos associar à expressão do cálculo da área do círculo, π * r². Partindo dessa associação podemos determinar a área de qualquer arco com a medida do raio e do ângulo central, através de uma simples regra de três. Observe:
Uma volta completa no círculo corresponde a 360º, valor que podemos associar à expressão do cálculo da área do círculo, π * r². Partindo dessa associação podemos determinar a área de qualquer arco com a medida do raio e do ângulo central, através de uma simples regra de três. Observe:
360º ————- π * r²
θº —————— x
Onde:
π = 3,14
r = raio do círculo
θº = medida do ângulo central
x = área do arco
Exemplo 1
Determine a área de um segmento circular com ângulo central de 32º e raio medindo 2 m.
Resolução:
360º ————- π * r²
32º —————— x
360x = 32 * π * r²
x = 32 * π * r² / 360
x = 32 * 3,14 * 2² / 360
x = 32 * 3,14 * 4 / 360
x = 401,92 / 360
x = 1,12
A área do segmento circular possui aproximadamente 1,12 m².
Exemplo 2
Qual a área de um setor circular com ângulo central medindo 120º e comprimento do raio igual a 12 metros.
360º ————- π * r²
120º —————— x
360x = 120 * π * r²
x = 120 * π * r² / 360
x = 120 * 3,14 * 12² / 360
x = 120 * 3,14 * 144 / 360
x = 54259,2 / 360
x = 150,7
A área do setor circular citado corresponde, aproximadamente, a 150,7 m².