COMPRIMENTO DA CIRCUNFERÊNCIA E ÁREA DE UM CÍRCULO
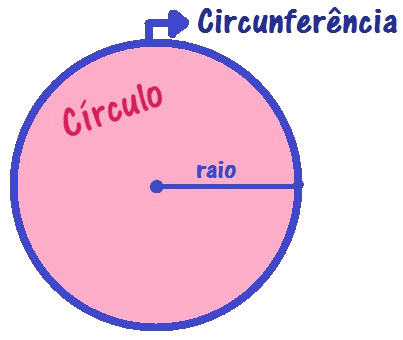
O comprimento da circunferência e a área de um círculo podem ser calculados em função do raio e do número irracional π.
A circunferência é um conjunto de pontos que estão a uma mesma distância do centro. Essa distância é conhecida como raio. A circunferência é estudada pela Geometria Analítica e, em geral, em um plano cartesiano. O círculo, que é formado pela circunferência e pelos infinitos pontos que preenchem seu interior, é estudado pela Geometria Plana, pois ele ocupa um espaço e pode ter sua área calculada, diferentemente da circunferência.
Para calcularmos o perímetro utilizando a seguinte definiçãoe: perímetro é a medida do contorno de um objeto. Nos polígonos o perímetro é dado a partir da soma de todos os seus lados. Já na circunferência o perímetro é obtido quando calculamos o seu comprimento.
Para calcular o comprimento de qualquer circunferência, precisamos conhecer a medida do raio (r). Conhecido o valor do raio, o comprimento da circunferência é dado pelo dobro do produto do raio por π (número irracional cujo valoraproximado é 3,14). Seja C o comprimento da circunferência, temos a seguinte fórmula:
C = 2·π·r
Mas se multiplicarmos o raio da circunferência por 2, encontraremos a medida dodiâmetro (segmento de reta que intercepta dois pontos da circunferência passando pelo centro). Seja d o diâmetro, também podemos utilizar a seguinte fórmula para calcular o comprimento da circunferência:
C = π·d
Como já dissemos, o círculo é uma figura plana, por isso podemos calcular sua área. Diferentemente das áreas limitadas por polígonos, não temos um valor para medidas de base ou de altura em um círculo. Por isso, para calcular a sua área, utilizamos a única informação que temos a seu respeito: o raio. A área de um círculo é dada pelo produto de π e do quadrado do raio. Seja A a área do círculo, temos a seguinte fórmula:
A = π·r²
Se o comprimento da circunferência for dado em cm, a área do círculo será dada em cm²; se o comprimento da circunferência for dado em m, a área do círculo será dada em m² e assim sucessivamente.
Por Amanda Gonçalves
Graduada em Matemática

